Ustalenie optymalnego układu lokalizacyjno-dystrybucyjnego dla wielu uczestników
- Marek Gubała
- Kategoria: Logistyka
Optymalizacja lokalizacji i rejonizacji w sieciach dystrybucji – cz. 2.
Ustalenie optymalnego układu lokalizacyjno-dystrybucyjnego dla wielu uczestników
Przyczyną rozwiązywania problemu wielu lokalizacji magazynów są następujące determinanty:
- skrócenie odległości dostawy,
- skrócenie czasu dostawy,
- podniesienie poziomu obsługi klienta poprzez umożliwienie wzajemnego uzupełnienia zapasów z zasobów okolicznych magazynów.
Planowanie przestrzenne lokalizacji magazynów dotyczy w szczególności przedsiębiorstw zorientowanych na wzrost dostępności produktów zarówno pod względem odległości (czasu dostawy), jak również utrzymania założonego poziomu obsługi klienta.
Wśród metod wspomagających decyzje dotyczące lokalizacji wielu magazynów możemy znaleźć mniej lub bardziej złożone i tym samym mniej lub bardziej precyzyjne. Jedną z nich jest metoda, której celem jest minimalizacja kosztów, polegająca na ustaleniu poprzez odpowiedni model matematyczny liczby produktów, jakie mają być dostarczane z rozważanych lokalizacji magazynów do poszczególnych odbiorców. Na podstawie analizy fundamentalnej wytypowano grupę magazynów o określonych (znanych) parametrach przestrzenno-geograficznych magazynów.
Danymi wejściowymi do modelu matematycznego rozpatrywanego w poniższym przykładzie są:
- pojemność Vi i koszt stały Ks utrzymania magazynów,
- macierz kosztów jednostkowych kj z i-tego magazynu do j-tego odbiorcy,
- znane jest także zapotrzebowanie Zj poszczególnych odbiorców.
Minimalizacja łącznego kosztu liczona jest z następującej formuły:
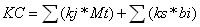 [1]
[1]
gdzie:
kj – koszt jednostkowy przewozu towaru z i-tego magazynu do j-tego odbiorcy,
Mt – masa przewożonego towaru w tonach,
Ks – koszt stały utrzymania magazynu,
bi – zmienna binarna (przyjmuje wartości 0 lub 1).
Przykład
Problem
Dana jest grupa siedmiu potencjalnych lokalizacji magazynów (d M1 do M7) oraz grupa ośmiu odbiorców obsługiwanych przez powyższe magazyny. Potencjał objętościowy hipotetycznych magazynów (Vi) wynosi 11300 m3 produktu x przy łącznym zapotrzebowaniu 8 odbiorców (od O1 do O8) na poziomie 4700 m3. Zgodnie z tabelą danych wejściowych (1) do przykładu, znane są następujące informacje:
Wśród metod wspomagających decyzje dotyczące lokalizacji wielu magazynów możemy znaleźć mniej lub bardziej złożone i tym samym mniej lub bardziej precyzyjne. Jedną z nich jest metoda, której celem jest minimalizacja kosztów, polegająca na ustaleniu poprzez odpowiedni model matematyczny liczby produktów, jakie mają być dostarczane z rozważanych lokalizacji magazynów do poszczególnych odbiorców. Na podstawie analizy fundamentalnej wytypowano grupę magazynów o określonych (znanych) parametrach przestrzenno-geograficznych magazynów.
Danymi wejściowymi do modelu matematycznego rozpatrywanego w poniższym przykładzie są:
- pojemność Vi i koszt stały Ks utrzymania magazynów,
- macierz kosztów jednostkowych kj z i-tego magazynu do j-tego odbiorcy,
- znane jest także zapotrzebowanie Zj poszczególnych odbiorców.
Minimalizacja łącznego kosztu liczona jest z następującej formuły:
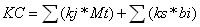 [1]
[1]gdzie:
kj – koszt jednostkowy przewozu towaru z i-tego magazynu do j-tego odbiorcy,
Mt – masa przewożonego towaru w tonach,
Ks – koszt stały utrzymania magazynu,
bi – zmienna binarna (przyjmuje wartości 0 lub 1).
Przykład
Problem
Dana jest grupa siedmiu potencjalnych lokalizacji magazynów (d M1 do M7) oraz grupa ośmiu odbiorców obsługiwanych przez powyższe magazyny. Potencjał objętościowy hipotetycznych magazynów (Vi) wynosi 11300 m3 produktu x przy łącznym zapotrzebowaniu 8 odbiorców (od O1 do O8) na poziomie 4700 m3. Zgodnie z tabelą danych wejściowych (1) do przykładu, znane są następujące informacje:
- pojemność magazynów (Vi),
- koszty stałe utrzymania magazynów (Ks),
- koszty jednostkowe dostawy (kj), produktu z i-tego magazynu do j-tego odbiorcy,
- zapotrzebowanie j-tych odbiorców.
Tabela 1. Dane wejściowe do przykładu
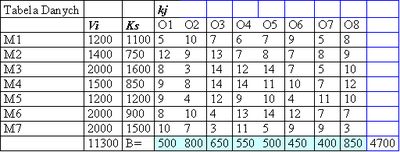
Spośród magazynów od M1 do M7 należy wybrać magazyny o optymalnie wykorzystanej objętości oraz najniższych kosztach całkowitych.
Analiza problemu
W rozwiązaniu zadania posłużymy się narzędziem Solver firmy Microsoft. W tym celu należy wprowadzić do arkusza kalkulacyjnego Excel tabelę (1) z danymi wejściowymi oraz dodatkowo utworzyć tabelę roboczą prezentowaną poniżej, zawierającą pola na wielkości.
Tabela 2. Tabela zmiennych decyzyjnych
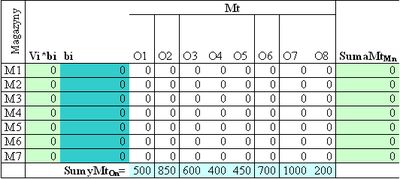
Ostatnio zmieniany w czwartek, 22 czerwiec 2006 16:30
Ściągnij załącznik:
Zaloguj się by skomentować


