Sterowanie wielkością zamówienia w Excelu - cz. 3
- Paweł Ślaski
- Kategoria: Logistyka
Artykuł wziął udział w III edycji Konkursu Piórem Logistyka.
4. Planowanie eksperymentów symulacyjnych
Podczas tego etapu ważne jest określenie typu rozkładu badanej charakterystyki. Dzięki tej informacji można będzie oszacować parametry rozkładu teoretycznego, przybliżanego dystrybuantą empiryczną. W opracowanym modelu identyfikacji typu rozkładu dokonano za pomocą tablicowania (rys. 6, 7). W wyniku pomiaru wartości określonych charakterystyk systemu (wielkości popytu i czasu realizacji zamówienia) otrzymuje się ciąg wartości opisany w kolumnie 2 (rys. 6 i 7).
Obserwacje można podzielić na : 

rozłącznych klas o tej samej długości równej: 

gdzie: 
 oznaczają kolejno: długość klasy, ilość klas, n-tą wartość charakterystyki ciągu uporządkowanego rosnąco, pierwszą wartość ciągu.
oznaczają kolejno: długość klasy, ilość klas, n-tą wartość charakterystyki ciągu uporządkowanego rosnąco, pierwszą wartość ciągu.

 oznaczają kolejno: długość klasy, ilość klas, n-tą wartość charakterystyki ciągu uporządkowanego rosnąco, pierwszą wartość ciągu.
oznaczają kolejno: długość klasy, ilość klas, n-tą wartość charakterystyki ciągu uporządkowanego rosnąco, pierwszą wartość ciągu.W związku z powyższym do r-tej klasy ( r=  ) należą te obserwacje, które spełniają nierówność:
) należą te obserwacje, które spełniają nierówność:
 ) należą te obserwacje, które spełniają nierówność:
) należą te obserwacje, które spełniają nierówność: <
< 
Środek klasy można wyznaczyć ze wzoru:

Po określeniu liczby klas, ilości elementów w klasie oraz środków klas należy, wykorzystując klasyczną definicję, ustalić prawdopodobieństwa klas. Pary: środek klasy oraz prawdopodobieństwo przynależności elementów do klas tworzą rozkład prawdopodobieństwa, który można zapisać w formie tablicy.
Do generowania liczb pseudolosowych o zidentyfikowanym rozkładzie (rys. 5,8) wykorzystano predefiniowaną funkcję arkusza f(x)=Los()3 (rys. 4). Generuje ona liczby z przedziału (0,1) zgodnie z rozkładem jednostajnym.
Wygenerowana liczba pomocnicza jest identyfikowana z odpowiednim numerem klasy (rys. 6,7). Środek otrzymanej klasy może być generowaną liczbą x o rozkładzie przedstawionym na wykresie (rys. 5,8). Model (rys. 4) pobiera wartości z dwóch tablic rozkładów (rys. 6,7): popytu oraz terminu realizacji zamówienia wraz z ich prawdopodobieństwami. Ich wartości generowane są w modelu za pomocą powyższej techniki.

Rys. 5. Rozkład prawdopodobieństwa wg klas dla popytu (opracowanie własne na podstawie: A. Manikowski, Z. Tarapata, Prognozowanie i symulacja rozwoju przedsiębiorstwa, WSE, Warszawa 2002)

Rys. 6. Stablicowany rozkład prawdopodobieństwa dla popytu (opracowanie własne na podstawie: A. Manikowski, Z. Tarapata, op. cit. )

Rys. 7. Stablicowany rozkład prawdopodobieństwa dla terminu realizacji zamówienia (opracowanie własne na podstawie: A. Manikowski, Z. Tarapata, op. cit.)
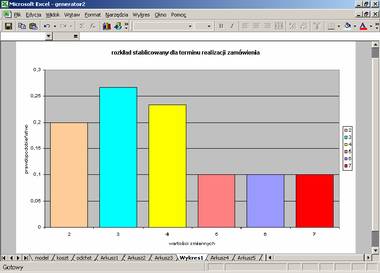
Rys. 8. Rozkład prawdopodobieństwa wg klas dla terminu realizacji zamówienia (opracowanie własne na podstawie: A. Manikowski, Z. Tarapata, op. cit.)
5. Analiza statystyczna wyników
Wyniki pojedynczej symulacji mogą być traktowane jako próba statystyczna. Trzeba jednak pamiętać o tym, że w wyniku przeprowadzenia drugiego eksperymentu, z innym zestawem niezależnych liczb pseudolosowych, oszacowania będą inne. Jest to spowodowane występowaniem elementów losowych w modelu. Właściwa ocena modelu polega na analizie wyników wielu eksperymentów oraz zastosowaniu kilku standardowych procedur. Należy oszacować parametr x funkcjonowania systemu (łączny, dzienny koszt zapasu) na podstawie wyników z n eksperymentów (przebiegów symulacji). Oszacowaniem oczekiwanej wielkości parametru x jest średnia arytmetyczna z uzyskanych wyników :
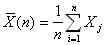
Odchylenie standardowe średniej arytmetycznej n niezależnych zmiennych losowych obliczymy ze wzoru :
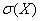 =
= 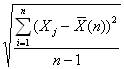
Uruchamiamy symulację za pomocą okna dialogowego przedstawionego na rys. 9.
Rys 9. Okno dialogowe dla symulacji (opracowanie własne)
Ostatnio zmieniany w poniedziałek, 29 październik 2007 11:27
Ściągnij załącznik:


